Introduction

The Insertion sort is one of the sorting algorithms used to organize the array's elements in a certain order. Bubble sort, Selection sort, Merge sort, Quick sort, Cycle sort, Radix sort, and additional sorting algorithms are available.

What is the process of sorting? Sorting is an operation on an array list that is used to arrange the array's contents in a certain order.

Today's topic will be insertion sort. We'll go to more places in the future.

Working Principle

Insertion sort is a straightforward algorithm for sorting data that organizes the array by first sorting a small range of indexes of the array. The number of indexes included inside the array that we are taking into consideration will grow exponentially.

Why insertion sort?

1. Adaptive: Steps or operations get reduced if the array is sorted. The number of swaps reduced as compared to bubble sort.

2. Stable

3. Works well for smaller values of the number of elements of the array

4. One of the best options for partially sorted arrays

5. It takes part in the hybrid sorting algorithm

Example

Okay, now let's be clear with this with an example.

This is the sample array we are considering. An array of 7 unsorted elements.

Here i and j denote the range of the array we are considering. Starting with the first two indexes.

Here 8 and 22 are already in their ideal situations. So we leave it alone and go on.

Now, we increase the range of indexes of the array we are considering.

We start comparing the last two adjacent elements. Now, 22 is bigger than 18, indicating that it is in the incorrect place. As a result, we switch the two numbers in their index.

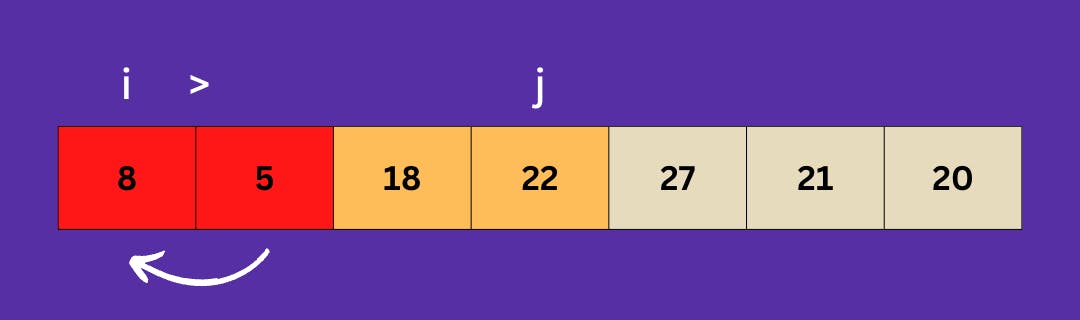
Now the range of indexes of the array we are considering is in a sorted manner. So we move on to increasing the range of the elements.

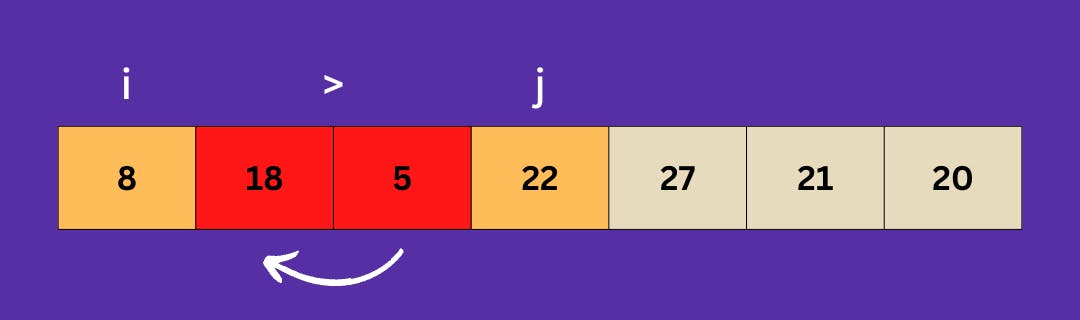
Now, we increase the range of indexes of the array we are considering. Adding 5 into consideration.

Now, 22 is bigger than 5, indicating that it is in the incorrect place. As a result, we switch the two numbers in their index.

Moving on to the next element, 18 is bigger than 5, indicating that it is in the incorrect place. As a result, we switch the two numbers in their index.

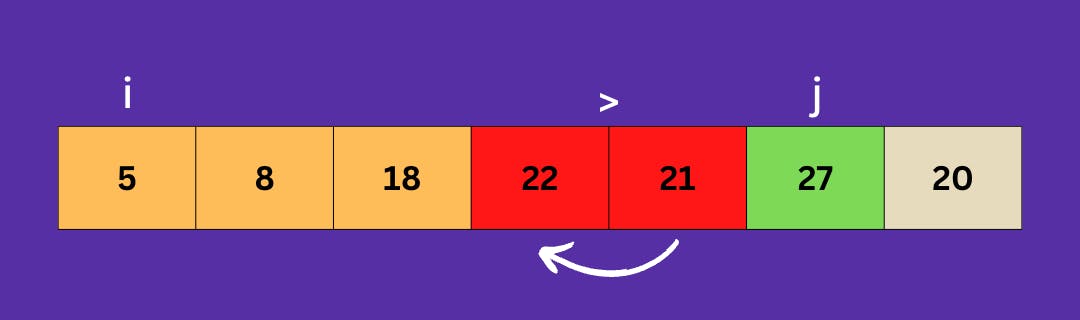
Also, 27 is greater than 20 so we swap them.

Now the range of indexes of the array we are considering is in a sorted manner. So we move on to increasing the range of the elements.

Doing the same for the rest of the array.

All the elements are in their ideal position so we move to next step.

Increasing the range of the elements

Comparing the elements

Swapping the wrong positions

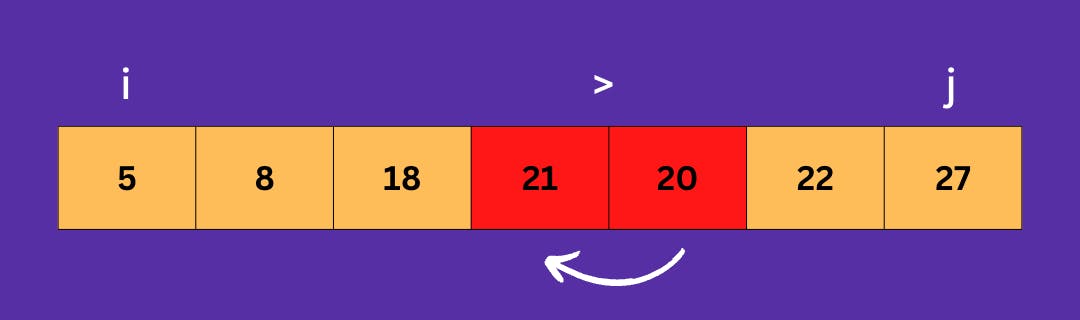
Now considering all the elements of the array.

Comparing.

Swapping, comparing.

Again swapping and comparing.

Now the array is completely sorted.

Sample Code

const insertionSort = (arr) =>{
    // Here i loop going only for n - 2 (1 element before last) because, j loop will run i + 1
    // So last elemnt will error index out of bound
    for(let i = 0; i <= arr.length - 2; i++){
        for(let j = i+1; j>0; j--){
            if(arr[j] < arr[j-1]){
                swap(arr, j, j-1);
            }else break;
        }
    }
    return arr;
}

// This is a helper function to swap two index position of the elements.
const swap = (arr, a, b) => {
  [arr[a], arr[b]] = [arr[b], arr[a]];
};

let myArr = [5, 3, 7, 1, 21, 8, 9, 4];
console.log(insertionSort(myArr));

//Output ->[ 1, 3, 4,  5, 7, 8, 9, 21 ]

Time and space complexity analysis

• In the end, each method is assessed based on its Big "O" notation. It is time and space complexity. The temporal complexity of the program determines how many operations it takes to complete the program. The space complexity of the program dictates how much auxiliary space (excluding the space needed for the input) is needed to run it.

• Because we are not creating a new array to sort this array, the space complexity remains unchanged.

• Time complexity is defined in two ways: best-case and worst-case scenarios.

• In the best case if the array is sorted then, T = O(N).

• In the worst case if the array is reversely sorted then, T = O(N ^ 2).