Introduction
The bubble sort is one of the sorting algorithms used to organize the array's elements in a particular order. Selection sort, Insertion sort, Merge sort, Quick sort, Cycle sort, Radix sort, and additional sorting algorithms are available.
Today's topic will be bubble sort. We'll go to more places in the future.
What is the process of sorting? Sorting is an array list operation used to arrange the array's contents in a particular order.
How does bubble sort work?
- The bubble sort is built on a comparison process. Bubble sort organizes the elements by continually comparing two adjacent elements to one another and swapping the numbers as needed.
Explanation
Here is a sample unsorted array containing 7 elements,

We begin with the first and second elements of index 0 and 1. We may go to the next index now that the first two components are correctly positioned.

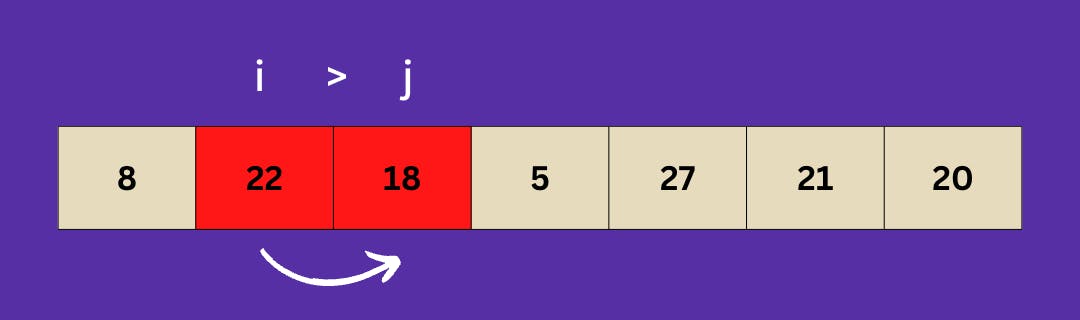
Now, 22 is bigger than 18, indicating that it is in the incorrect place. As a result, we switch the two numbers in their index.

Moving on to the next index, we can see that 22 is more than 5. As a result, we switch them to number positions. And now we're going on.

22 and 27 are in ideal situations. So we leave it alone and go on.
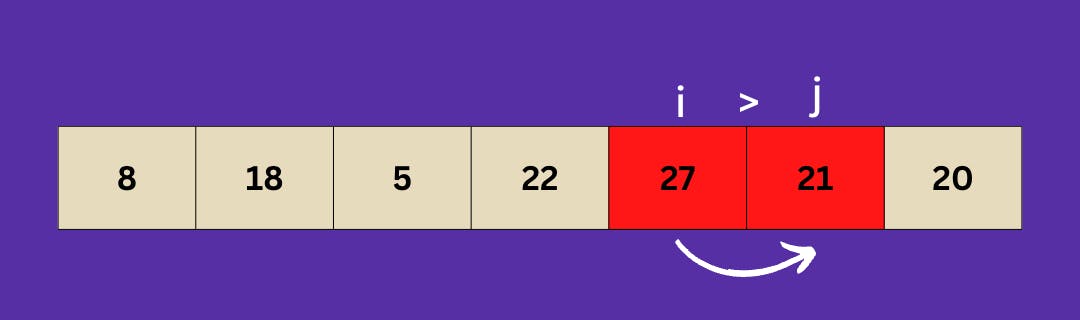
But 27 is greater than 21, so we swap them.
Also, 27 is greater than 20, so we swap them.

Now the first iteration is completed. We should move on to the next iteration.


The first two numbers are in their correct position, we move on to the next one.

Now, 18 is more than 5, indicating that it is in the incorrect place. As a result, we switch the two numbers in their index.

18 and 22 are in their perfect positions. So we leave it untouched and move on.

Now, 22 is greater than 21, which indicates its wrong position. So, we swap the two numbers from their index.
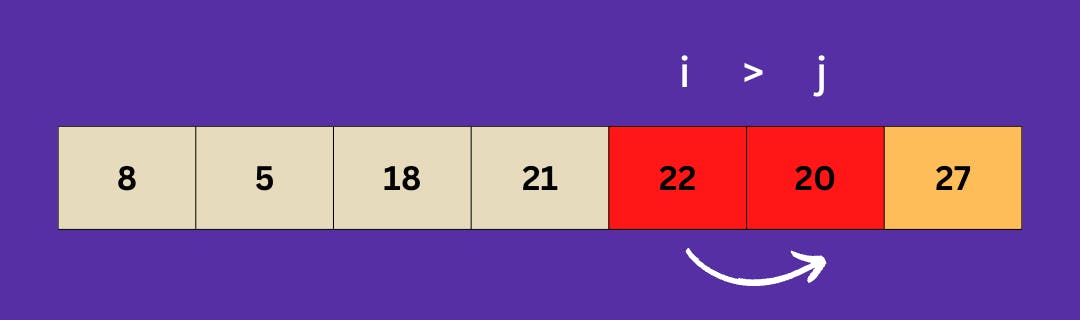
Moving on to the next index, we can see that 22 is greater than 20. As a result, we switch them to number positions. And now we're going on.

You'll note that the array is now sorting from the right side. In addition, the greatest number is assigned to its spot. As a result, we ignore the sorted part of the array for each iteration.
Now do the same for the remaining array.

Wrong position, swap.

Correct position. Leave. Move on.

Correct position. Leave. Move on.

Wrong position, swap.

If no changes have been made throughout the iteration, then stop and return.

Correct position. Leave. Move on.

Correct position. Leave. Move on.


Now all the array elements are in the correct position.
Sample Code
const bubbleSort = (arr) =>{
let swapped;
for(let x=0; x<arr.length; x++){
swapped = false;
for(let i=1; i<arr.length - x; i++){
if(arr[i] < arr[i - 1]){
swap(arr, i-1, i)
swapped = true;
}
}
//If no changes have been made, stop and return
if (!swapped) break;
}
return arr;
}
const swap = (arr, i, j) =>{
[arr[i], arr[j]] = [arr[j], arr[i]];
}
let arr = [1, 7, 10, 3, 4, 5];
console.log(bubbleSort(arr));
// [ 1, 3, 4, 5, 7, 10 ]
Conclusion
In the end, each method is valued based on its Big "O" notation. It is time and space complexity. The temporal complexity of the program determines how long it takes to execute. The space complexity of the software dictates how much space is needed to run it.
Because we are not creating a new array to sort this array, the space complexity remains unchanged.
Time complexity is defined in two ways: best-case and worst-case scenarios.
In the best case (if the array is sorted then), T = O(N).
In the worst case (if the array is reversely sorted then), T = O(N ^ 2).
